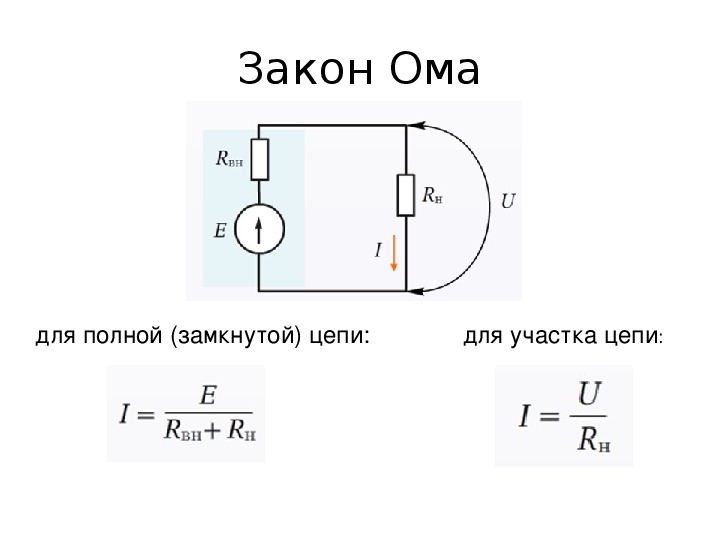
- क्लोज्ड सर्किट के लिए
- अलग सेक्शन और पूरा इलेक्ट्रिकल सर्किट
- विद्युत परिपथ के वर्तमान खंड की गणना
- एक पूरी श्रृंखला के लिए गणना विकल्प
- एक चर पर कानून का प्रभाव
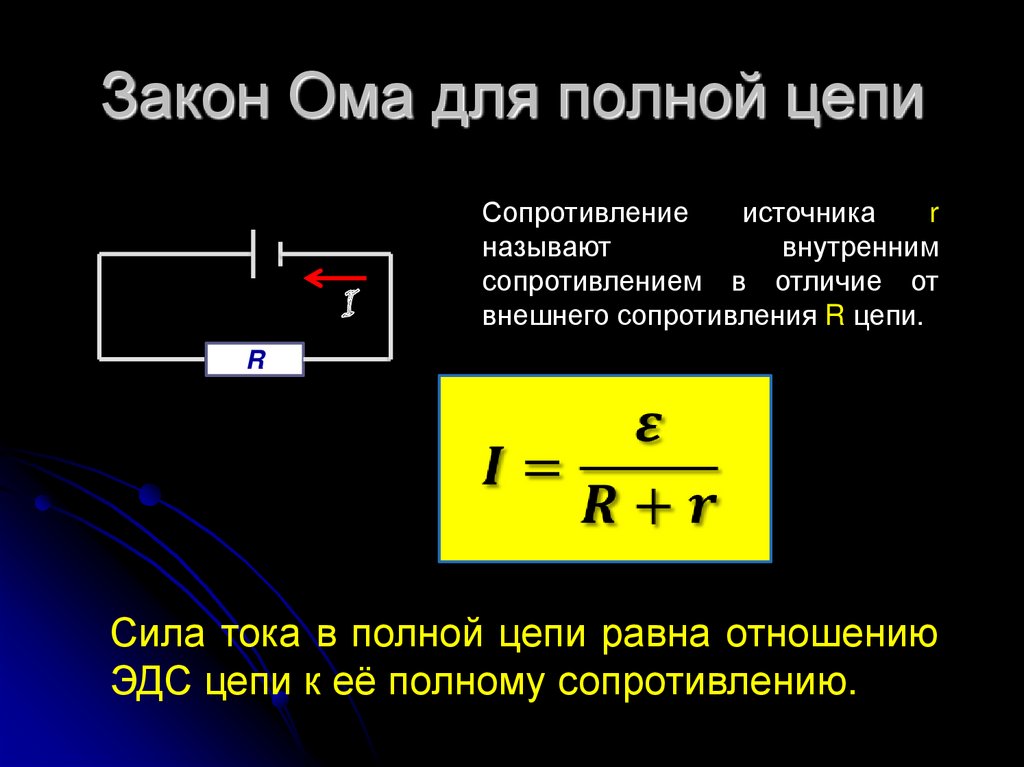
- एक पूर्ण परिपथ में EMF स्रोत
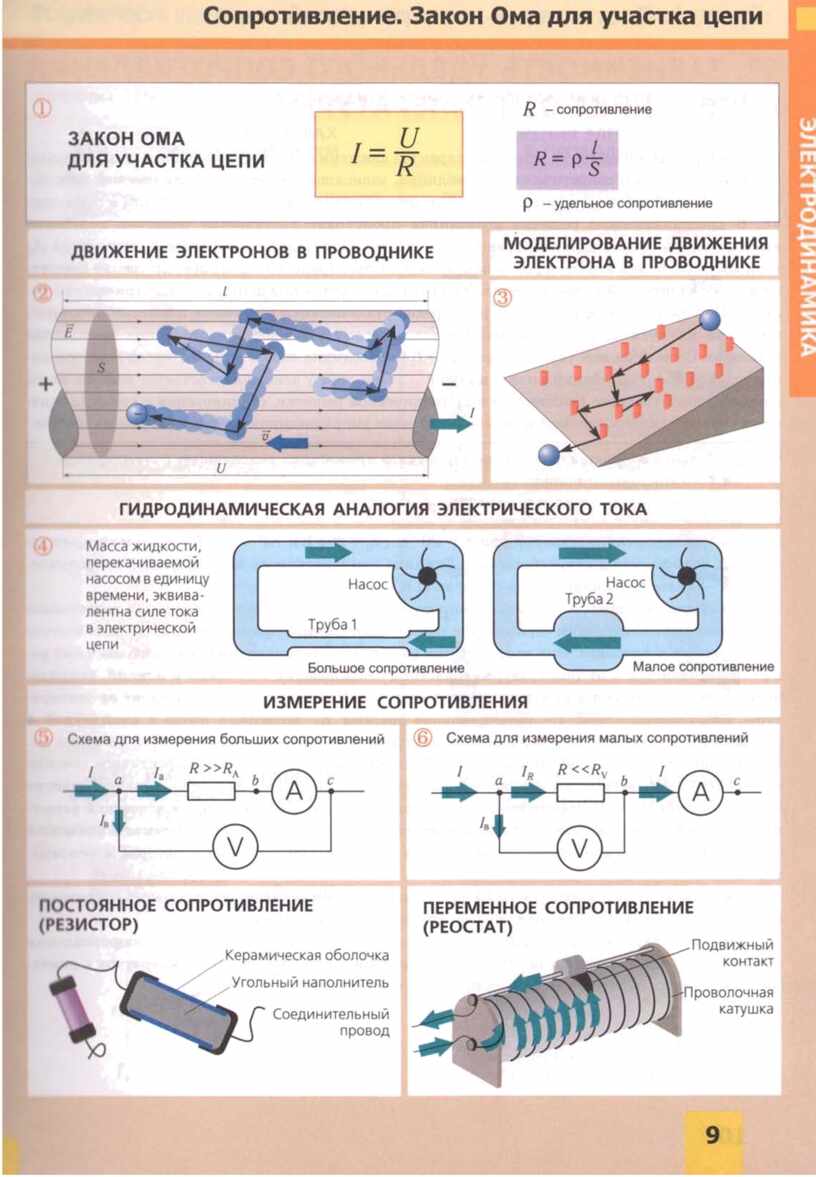
- आर - विद्युत प्रतिरोध
- डीसी सर्किट का गैर-समान खंड
- तत्वों का सीरियल और समानांतर कनेक्शन
- श्रृंखला से जुड़े प्रतिरोधक तत्वों की एक श्रृंखला
- समानांतर जुड़े प्रतिरोधक तत्वों की एक श्रृंखला
- कानून के अभिन्न और विभेदक रूप
- वर्तमान और प्रतिरोध को समझना
- प्रत्यावर्ती धारा के लिए ओम का नियम
- जब ओम का नियम होता है
- किरचॉफ के नियम।
- मूल अवधारणा
- ताकत और तनाव
- कंडक्टर प्रतिरोध
- ओम के नियम की व्याख्या
- समानांतर और सीरियल कनेक्शन
- सीरियल कनेक्शन
- समानांतर कनेक्शन
- क्या हमें समानांतर और सीरियल कनेक्शन देता है?
- आदर्श ईएमएफ स्रोत
- विभेदक रूप में
क्लोज्ड सर्किट के लिए
क्लोज्ड सर्किट का अर्थ है एक बंद विद्युत कनेक्शन जिसके माध्यम से करंट प्रवाहित होता है। जब तारों की एक श्रृंखला एक दूसरे से जुड़ती है और सर्किट को पूरा करती है ताकि मैं सर्कल के एक छोर से दूसरे छोर तक चला जाऊं, यह एक बंद सर्किट होगा।
ईएमएफ (ई) - वोल्ट में निरूपित और मापा जाता है और फैराडे के नियम के अनुसार बैटरी या चुंबकीय बल द्वारा उत्पन्न वोल्टेज को संदर्भित करता है, जिसमें कहा गया है कि एक समय-भिन्न चुंबकीय क्षेत्र विद्युत प्रवाह को प्रेरित करेगा।
तब: ई = आईआर + इर
ई \u003d मैं (आर + आर)
मैं \u003d ई / (आर + आर)
कहा पे: r वर्तमान स्रोत का प्रतिरोध है।
इस व्यंजक को बंद लूप परिपथों के ओम के नियम के रूप में जाना जाता है।
विषम श्रृंखला
अलग सेक्शन और पूरा इलेक्ट्रिकल सर्किट
ओम का नियम, जैसा कि एक खंड या पूरे सर्किट पर लागू होता है, दो गणना विकल्पों में माना जा सकता है:
- अलग लघु खंड। यह एक EMF स्रोत के बिना सर्किट का हिस्सा है।
- एक या अधिक वर्गों से युक्त एक पूरी श्रृंखला। इसमें एक ईएमएफ स्रोत भी शामिल है जिसका अपना आंतरिक प्रतिरोध है।
विद्युत परिपथ के वर्तमान खंड की गणना
इस मामले में, मूल सूत्र I \u003d U / R लागू होता है, जिसमें I वर्तमान ताकत है, U वोल्टेज है, R प्रतिरोध है। इसके अनुसार, ओम के नियम की आम तौर पर स्वीकृत व्याख्या तैयार की जा सकती है:
यह सूत्रीकरण ग्राफिक डिजाइन में तथाकथित "कैमोमाइल" पर प्रस्तुत कई अन्य सूत्रों का आधार है। सेक्टर P में - शक्ति निर्धारित की जाती है, सेक्टर I, U और R में - वर्तमान शक्ति, वोल्टेज और प्रतिरोध से संबंधित क्रियाएं की जाती हैं।
प्रत्येक अभिव्यक्ति - मूल और अतिरिक्त दोनों, आपको सर्किट में उपयोग के लिए इच्छित तत्वों के सटीक मापदंडों की गणना करने की अनुमति देती है।
विद्युत सर्किट के साथ काम करने वाले विशेषज्ञ चित्र में दिखाए गए त्रिकोण विधि का उपयोग करके किसी भी पैरामीटर का त्वरित निर्धारण करते हैं।
गणना को अनुभाग के तत्वों को जोड़ने वाले कंडक्टरों के प्रतिरोध को ध्यान में रखना चाहिए। चूंकि वे विभिन्न सामग्रियों से बने होते हैं, इसलिए यह पैरामीटर प्रत्येक मामले में अलग होगा।यदि एक पूर्ण सर्किट बनाना आवश्यक है, तो मुख्य सूत्र एक वोल्टेज स्रोत के मापदंडों के साथ पूरक है, उदाहरण के लिए, एक बैटरी।
एक पूरी श्रृंखला के लिए गणना विकल्प
एक पूर्ण सर्किट में अलग-अलग खंड होते हैं, जो एक वोल्टेज स्रोत (ईएमएफ) के साथ मिलकर एक पूरे में संयुक्त होते हैं। इस प्रकार, वर्गों के मौजूदा प्रतिरोध को जुड़े स्रोत के आंतरिक प्रतिरोध द्वारा पूरक किया जाता है। इसलिए, पहले चर्चा की गई मुख्य व्याख्या इस प्रकार पढ़ेगी: I = U / (R + r)। यहां, ईएमएफ स्रोत का प्रतिरोधक संकेतक (आर) पहले ही जोड़ा जा चुका है।
शुद्ध भौतिकी की दृष्टि से इस सूचक को बहुत छोटा मान माना जाता है। हालांकि, व्यवहार में, जटिल सर्किट और सर्किट की गणना करते समय, विशेषज्ञों को इसे ध्यान में रखना पड़ता है, क्योंकि अतिरिक्त प्रतिरोध काम की सटीकता को प्रभावित करता है। इसके अलावा, प्रत्येक स्रोत की संरचना बहुत विषम है, परिणामस्वरूप, कुछ मामलों में प्रतिरोध काफी उच्च दरों द्वारा व्यक्त किया जा सकता है।
उपरोक्त गणना डीसी सर्किट के संबंध में की जाती है। प्रत्यावर्ती धारा के साथ क्रिया और गणना एक अलग योजना के अनुसार की जाती है।
एक चर पर कानून का प्रभाव
प्रत्यावर्ती धारा के साथ, सर्किट का प्रतिरोध तथाकथित प्रतिबाधा होगा, जिसमें सक्रिय प्रतिरोध और प्रतिक्रियाशील प्रतिरोधक भार शामिल होंगे। यह आगमनात्मक गुणों वाले तत्वों की उपस्थिति और एक साइनसॉइडल वर्तमान मूल्य के कारण है। वोल्टेज भी एक चर है, जो इसके स्विचिंग कानूनों के अनुसार कार्य करता है।
इसलिए, ओम के नियम एसी सर्किट डिजाइन की गणना विशिष्ट प्रभावों को ध्यान में रखते हुए की जाती है: वोल्टेज से करंट के परिमाण को आगे या पीछे करना, साथ ही साथ सक्रिय और प्रतिक्रियाशील शक्ति की उपस्थिति।बदले में, प्रतिक्रिया में आगमनात्मक या कैपेसिटिव घटक शामिल होते हैं।
ये सभी घटनाएं सूत्र Z \u003d U / I या Z \u003d R + J * (XL - XC) के अनुरूप होंगी, जिसमें Z प्रतिबाधा है; आर - सक्रिय भार; एक्सएल, एक्ससी - आगमनात्मक और कैपेसिटिव भार; J सुधार कारक है।
एक पूर्ण परिपथ में EMF स्रोत
बंद परिपथ में विद्युत धारा की घटना के लिए, इस परिपथ में कम से कम एक विशेष तत्व होना चाहिए जिसमें इसके ध्रुवों के बीच आवेशों को स्थानांतरित करने का कार्य होगा। इस तत्व के अंदर आवेशों को ले जाने वाले बल विद्युत क्षेत्र के विरुद्ध ऐसा करते हैं, जिसका अर्थ है कि उनकी प्रकृति विद्युत से भिन्न होनी चाहिए। इसलिए, ऐसी ताकतों को तृतीय-पक्ष कहा जाता है।
चावल। 1. भौतिकी में बाहरी बल।
विद्युत परिपथ का वह तत्व जिसमें बाह्य बल विद्युत क्षेत्र की क्रिया के विरुद्ध आवेशों को स्थानांतरित करने का कार्य करते हैं, धारा स्रोत कहलाते हैं। इसकी मुख्य विशेषता बाहरी ताकतों का परिमाण है। इसे चिह्नित करने के लिए, एक विशेष उपाय पेश किया जाता है - इलेक्ट्रोमोटिव फोर्स (ईएमएफ), इसे अक्षर $\mathscr{E}$ द्वारा दर्शाया जाता है।
वर्तमान स्रोत के ईएमएफ का मूल्य इस चार्ज के मूल्य के लिए चार्ज के हस्तांतरण के लिए बाहरी बलों के अनुपात के बराबर है:
$$\mathscr{E}={A_{st}\over q}$$
चूंकि EMF का अर्थ विद्युत वोल्टेज के अर्थ के बहुत करीब है (याद रखें, वोल्टेज विद्युत क्षेत्र द्वारा किए गए कार्य का अनुपात है जो चार्ज को इस चार्ज के मान तक ले जाता है), तो EMF, वोल्टेज की तरह, में मापा जाता है वोल्ट:
$$1B={J\overCl}$$
एक वास्तविक वर्तमान स्रोत की दूसरी सबसे महत्वपूर्ण विद्युत विशेषता इसका आंतरिक प्रतिरोध है।जब चार्ज टर्मिनलों के बीच स्थानांतरित होते हैं, तो वे ईएमएफ स्रोत के पदार्थ के साथ बातचीत करते हैं, और इसलिए, विद्युत प्रवाह का स्रोत भी कुछ प्रतिरोध प्रस्तुत करता है। आंतरिक प्रतिरोध, सामान्य प्रतिरोध की तरह, ओम में मापा जाता है, लेकिन इसे छोटे लैटिन अक्षर $r$ द्वारा दर्शाया जाता है।

चावल। 2. वर्तमान स्रोतों के उदाहरण।
आर - विद्युत प्रतिरोध
प्रतिरोध वोल्टेज का पारस्परिक है और इसकी तुलना बहते पानी में गति के विरुद्ध शरीर को हिलाने के प्रभाव से की जा सकती है। R की इकाई ओम है, जिसे बड़े ग्रीक अक्षर ओमेगा द्वारा दर्शाया जाता है।
प्रतिरोध के पारस्परिक (1/R) को चालकता के रूप में जाना जाता है, जो सीमेंस इकाइयों में व्यक्त किए गए आवेश को संचालित करने के लिए किसी वस्तु की क्षमता को मापता है।
ज्यामितीय रूप से उपयोग की जाने वाली स्वतंत्र मात्रा को प्रतिरोधकता कहा जाता है और इसे आमतौर पर ग्रीक प्रतीक r द्वारा दर्शाया जाता है।
अतिरिक्त जानकारी। ओम का नियम विद्युत नेटवर्क के संचालन के तीन महत्वपूर्ण संकेतक स्थापित करने में मदद करता है, जो शक्ति की गणना को सरल करता है। यह डायोड, ट्रांजिस्टर और इसी तरह के तत्वों वाले एकतरफा नेटवर्क पर लागू नहीं होता है। और यह गैर-रैखिक तत्वों पर भी लागू नहीं होता है, जिनमें से थाइरिस्टर उदाहरण हैं, क्योंकि इन तत्वों का प्रतिरोध मान अलग-अलग वोल्टेज और करंट के साथ बदलता है।
उच्च आवृत्तियों पर, वितरित व्यवहार प्रभावी हो जाता है। बहुत लंबी बिजली लाइनों के साथ भी यही होता है। यहां तक कि 60 हर्ट्ज जितनी कम आवृत्ति पर, एक बहुत लंबी ट्रांसमिशन लाइन, जैसे कि 30 किमी, में एक वितरित प्रकृति होती है।इसका मुख्य कारण यह है कि सर्किट में फैलने वाले प्रभावी विद्युत संकेत विद्युत चुम्बकीय तरंगें हैं, न कि वोल्ट और एम्पीयर, जो विद्युत चुम्बकीय तरंग से संक्रमित होते हैं। कंडक्टर केवल तरंगों के लिए मार्गदर्शक के रूप में कार्य करते हैं। इसलिए, उदाहरण के लिए, एक समाक्षीय केबल Z = 75 ओम दिखाएगा, भले ही इसका DC प्रतिरोध नगण्य हो।
ओम का नियम इलेक्ट्रिकल इंजीनियरिंग का मौलिक नियम है। इसमें सभी विद्युत परिपथों और इलेक्ट्रॉनिक घटकों में बड़ी संख्या में व्यावहारिक अनुप्रयोग हैं।
ओम के नियम को लागू करने के सबसे सामान्य उदाहरण:
- बिजली के हीटर को आपूर्ति की गई बिजली। हीटर कॉइल के प्रतिरोध और लागू वोल्टेज को देखते हुए, उस हीटर को आपूर्ति की जाने वाली शक्ति की गणना की जा सकती है।
- फ़्यूज़ का विकल्प। वे सुरक्षा घटक हैं जो इलेक्ट्रॉनिक उपकरणों के साथ श्रृंखला में जुड़े हुए हैं। फ़्यूज़/सीबी को एम्पीयर में रेट किया गया है। वर्तमान फ्यूज रेटिंग की गणना ओम के नियम का उपयोग करके की जाती है।
- इलेक्ट्रॉनिक उपकरणों का डिजाइन। लैपटॉप और मोबाइल फोन जैसे इलेक्ट्रॉनिक उपकरणों को एक विशिष्ट वर्तमान रेटिंग के साथ डीसी बिजली की आपूर्ति की आवश्यकता होती है। विशिष्ट मोबाइल फोन की बैटरी के लिए 0.7-1A की आवश्यकता होती है। इन घटकों के माध्यम से प्रवाहित होने वाली धारा की दर को नियंत्रित करने के लिए एक अवरोधक का उपयोग किया जाता है। ओम के नियम का उपयोग एक विशिष्ट परिपथ में रेटेड धारा की गणना के लिए किया जाता है।
एक समय में, ओम के निष्कर्ष बिजली के क्षेत्र में नए शोध के लिए उत्प्रेरक बन गए, और आज उन्होंने अपना महत्व नहीं खोया है, क्योंकि आधुनिक इलेक्ट्रिकल इंजीनियरिंग उन पर आधारित है। 1841 में, ओम को रॉयल सोसाइटी के सर्वोच्च सम्मान, कोपले मेडल से सम्मानित किया गया था, और "ओम" शब्द को 1872 की शुरुआत में प्रतिरोध की एक इकाई के रूप में मान्यता दी गई थी।
डीसी सर्किट का गैर-समान खंड
एक विषम संरचना में सर्किट का ऐसा खंड होता है, जहां कंडक्टर और तत्वों के अलावा, एक वर्तमान स्रोत होता है। इस क्षेत्र में कुल वर्तमान ताकत की गणना करते समय इसकी ईएमएफ को ध्यान में रखा जाना चाहिए।
एक सूत्र है जो एक विषम साइट के मुख्य मापदंडों और प्रक्रियाओं को परिभाषित करता है: q = q0 x n x V। इसके संकेतक इस प्रकार हैं:
- गतिमान आवेशों (q) की प्रक्रिया में, वे एक निश्चित घनत्व प्राप्त कर लेते हैं। इसका प्रदर्शन कंडक्टर (एस) की वर्तमान ताकत और क्रॉस-सेक्शनल क्षेत्र पर निर्भर करता है।
- एक निश्चित एकाग्रता (एन) की शर्तों के तहत, एक ही समय में स्थानांतरित किए गए यूनिट चार्ज (क्यू 0) की संख्या को सटीक रूप से इंगित करना संभव है।
- गणना के लिए, कंडक्टर को सशर्त रूप से कुछ मात्रा (वी) के साथ एक बेलनाकार खंड माना जाता है।
कंडक्टर को बैटरी से कनेक्ट करते समय, बाद वाले को थोड़ी देर बाद डिस्चार्ज कर दिया जाएगा। यानी इलेक्ट्रॉनों की गति धीरे-धीरे धीमी हो जाती है और अंत में पूरी तरह से रुक जाती है। यह कंडक्टर के आणविक जाली द्वारा सुगम होता है, जो एक दूसरे और अन्य कारकों के साथ इलेक्ट्रॉनों की टक्कर का प्रतिकार करता है। इस तरह के प्रतिरोध को दूर करने के लिए, कुछ तृतीय-पक्ष बलों को अतिरिक्त रूप से लागू किया जाना चाहिए।
गणना के दौरान, इन बलों को कूलम्ब वाले में जोड़ा जाता है। इसके अलावा, यूनिट चार्ज q को 1 बिंदु से दूसरे स्थान पर स्थानांतरित करने के लिए, कार्य A1-2 या केवल A12 करना आवश्यक होगा। इस प्रयोजन के लिए, एक संभावित अंतर (ϕ1 - ϕ2) बनाया जाता है। एक प्रत्यक्ष वर्तमान स्रोत की कार्रवाई के तहत, एक ईएमएफ उत्पन्न होता है, जो सर्किट के साथ चार्ज करता है। कुल तनाव के परिमाण में ऊपर उल्लिखित सभी बल शामिल होंगे।
गणना में डीसी आपूर्ति के कनेक्शन की ध्रुवीयता को ध्यान में रखा जाना चाहिए। जब टर्मिनलों को बदल दिया जाता है, तो ईएमएफ भी बदल जाएगा, शुल्कों की गति को तेज या धीमा कर देगा।
तत्वों का सीरियल और समानांतर कनेक्शन
विद्युत परिपथ (सर्किट का खंड) के तत्वों के लिए, एक विशिष्ट क्षण एक श्रृंखला या समानांतर कनेक्शन है।
तदनुसार, प्रत्येक प्रकार का कनेक्शन वर्तमान प्रवाह और वोल्टेज आपूर्ति की एक अलग प्रकृति के साथ होता है। इस खाते पर, तत्वों को शामिल करने के विकल्प के आधार पर, ओम का नियम भी अलग-अलग तरीकों से लागू होता है।
श्रृंखला से जुड़े प्रतिरोधक तत्वों की एक श्रृंखला
एक श्रृंखला कनेक्शन (दो घटकों के साथ एक सर्किट का खंड) के संबंध में, शब्द का प्रयोग किया जाता है:
- मैं = मैं1 = मैं2 ;
- यू = यू1 + यू2 ;
- आर = आर1 + आर2
यह सूत्रीकरण स्पष्ट रूप से दर्शाता है कि, श्रृंखला में जुड़े प्रतिरोधक घटकों की संख्या की परवाह किए बिना, सर्किट के एक खंड में प्रवाहित होने वाली धारा का मान नहीं बदलता है।
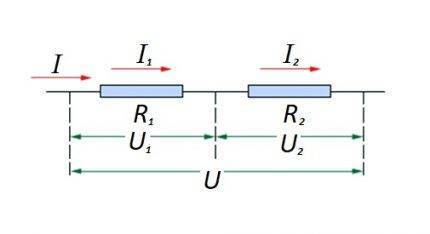 एक सर्किट सेक्शन में प्रतिरोधक तत्वों को एक दूसरे के साथ श्रृंखला में जोड़ना। इस विकल्प का अपना गणना कानून है। आरेख में: I, I1, I2 - वर्तमान प्रवाह; R1, R2 - प्रतिरोधक तत्व; यू, यू1, यू2 - लागू वोल्टेज
एक सर्किट सेक्शन में प्रतिरोधक तत्वों को एक दूसरे के साथ श्रृंखला में जोड़ना। इस विकल्प का अपना गणना कानून है। आरेख में: I, I1, I2 - वर्तमान प्रवाह; R1, R2 - प्रतिरोधक तत्व; यू, यू1, यू2 - लागू वोल्टेज
सर्किट के सक्रिय प्रतिरोधी घटकों पर लागू वोल्टेज की मात्रा योग है और ईएमएफ स्रोत के मूल्य में जोड़ती है।
इस मामले में, प्रत्येक व्यक्तिगत घटक पर वोल्टेज है: Ux = I * Rx।
कुल प्रतिरोध को सर्किट के सभी प्रतिरोधक घटकों के मूल्यों के योग के रूप में माना जाना चाहिए।
समानांतर जुड़े प्रतिरोधक तत्वों की एक श्रृंखला
उस स्थिति में जब प्रतिरोधक घटकों का समानांतर संबंध होता है, जर्मन भौतिक विज्ञानी ओम के कानून के संबंध में सूत्रीकरण को उचित माना जाता है:
- मैं = मैं1 + मैं2 … ;
- यू = यू1 = यू2 … ;
- 1/आर = 1/आर1 + 1 / आर2 + …
समानांतर और सीरियल कनेक्शन का उपयोग करते समय "मिश्रित" प्रकार के सर्किट अनुभागों को संकलित करने के विकल्पों को बाहर नहीं किया जाता है।
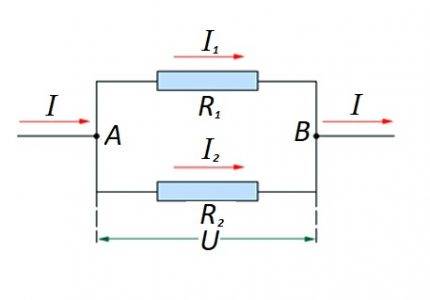 एक दूसरे के समानांतर सर्किट सेक्शन में प्रतिरोधक तत्वों का कनेक्शन। इस विकल्प के लिए, इसका अपना गणना कानून लागू होता है। आरेख में: I, I1, I2 - वर्तमान प्रवाह; R1, R2 - प्रतिरोधक तत्व; यू - लागू वोल्टेज; ए, बी - प्रवेश / निकास बिंदु
एक दूसरे के समानांतर सर्किट सेक्शन में प्रतिरोधक तत्वों का कनेक्शन। इस विकल्प के लिए, इसका अपना गणना कानून लागू होता है। आरेख में: I, I1, I2 - वर्तमान प्रवाह; R1, R2 - प्रतिरोधक तत्व; यू - लागू वोल्टेज; ए, बी - प्रवेश / निकास बिंदु
ऐसे विकल्पों के लिए, गणना आमतौर पर समानांतर कनेक्शन की प्रतिरोधक रेटिंग की प्रारंभिक गणना द्वारा की जाती है। फिर श्रृंखला में जुड़े रोकनेवाला का मान परिणाम में जोड़ा जाता है।
कानून के अभिन्न और विभेदक रूप
गणना के साथ उपरोक्त सभी बिंदु उन स्थितियों पर लागू होते हैं जब "सजातीय" संरचना के कंडक्टर, इसलिए बोलने के लिए, विद्युत सर्किट के हिस्से के रूप में उपयोग किए जाते हैं।
इस बीच, व्यवहार में, अक्सर एक योजनाबद्ध के निर्माण से निपटना पड़ता है, जहां विभिन्न क्षेत्रों में कंडक्टरों की संरचना बदलती है। उदाहरण के लिए, एक बड़े क्रॉस सेक्शन के तारों का उपयोग किया जाता है या, इसके विपरीत, छोटे वाले, विभिन्न सामग्रियों के आधार पर बनाए जाते हैं।
इस तरह के मतभेदों को ध्यान में रखते हुए, तथाकथित "डिफरेंशियल-इंटीग्रल ओम के नियम" में भिन्नता है। एक असीम रूप से छोटे कंडक्टर के लिए, वर्तमान घनत्व स्तर की गणना तीव्रता और चालकता मूल्य के आधार पर की जाती है।
अंतर गणना के तहत, सूत्र लिया जाता है: जे = * ई
अभिन्न गणना के लिए, क्रमशः, सूत्रीकरण: I * R = φ1 - φ2 +
हालाँकि, ये उदाहरण उच्च गणित के स्कूल के काफी करीब हैं और वास्तव में एक साधारण इलेक्ट्रीशियन के वास्तविक अभ्यास में उपयोग नहीं किए जाते हैं।
वर्तमान और प्रतिरोध को समझना
आइए विद्युत प्रवाह की अवधारणा से शुरू करते हैं।संक्षेप में, धातुओं के संबंध में विद्युत प्रवाह इलेक्ट्रॉनों की निर्देशित गति है - नकारात्मक रूप से आवेशित कण। उन्हें आमतौर पर छोटे हलकों के रूप में दर्शाया जाता है। एक शांत अवस्था में, वे लगातार अपनी दिशा बदलते हुए, बेतरतीब ढंग से आगे बढ़ते हैं। कुछ शर्तों के तहत - एक संभावित अंतर की उपस्थिति - ये कण किसी दिशा में एक निश्चित गति शुरू करते हैं। यह गति विद्युत प्रवाह है।
इसे स्पष्ट करने के लिए, हम इलेक्ट्रॉनों की तुलना किसी समतल पर गिराए गए पानी से कर सकते हैं। जब तक विमान स्थिर है, पानी नहीं हिलता। लेकिन, जैसे ही एक ढलान दिखाई दिया (एक संभावित अंतर उत्पन्न हुआ), पानी चलना शुरू हो गया। इलेक्ट्रॉनों के साथ भी ऐसा ही है।
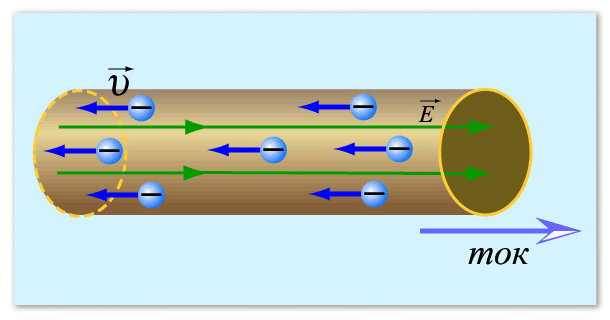
इस प्रकार विद्युत धारा की कल्पना की जा सकती है
अब हमें यह समझने की जरूरत है कि प्रतिरोध क्या है और उनके पास वर्तमान ताकत के साथ प्रतिक्रिया क्यों है: प्रतिरोध जितना अधिक होगा, वर्तमान उतना ही कम होगा। जैसा कि आप जानते हैं, इलेक्ट्रॉन एक चालक के माध्यम से चलते हैं। आमतौर पर ये धातु के तार होते हैं, क्योंकि धातुओं में बिजली का संचालन करने की अच्छी क्षमता होती है। हम जानते हैं कि धातु में एक सघन क्रिस्टल जाली होती है: कई कण जो करीब और परस्पर जुड़े होते हैं। धातु के परमाणुओं के बीच अपना रास्ता बनाते हुए इलेक्ट्रॉन उनसे टकराते हैं, जिससे उनका हिलना-डुलना मुश्किल हो जाता है। यह उस प्रतिरोध को स्पष्ट करने में मदद करता है जो एक कंडक्टर लगाता है। अब यह स्पष्ट हो जाता है कि प्रतिरोध जितना अधिक होता है, वर्तमान शक्ति उतनी ही कम होती है - जितने अधिक कण, इलेक्ट्रॉनों के लिए पथ को पार करना उतना ही कठिन होता है, वे इसे और अधिक धीरे-धीरे करते हैं। ऐसा लगता है कि इसे सुलझा लिया गया है।
यदि आप अनुभवजन्य रूप से इस निर्भरता का परीक्षण करने की इच्छा रखते हैं, तो एक चर रोकनेवाला खोजें, श्रृंखला में एक रोकनेवाला - एक एमीटर - एक वर्तमान स्रोत (बैटरी) से कनेक्ट करें।सर्किट में एक स्विच सम्मिलित करना भी वांछनीय है - एक साधारण टॉगल स्विच।
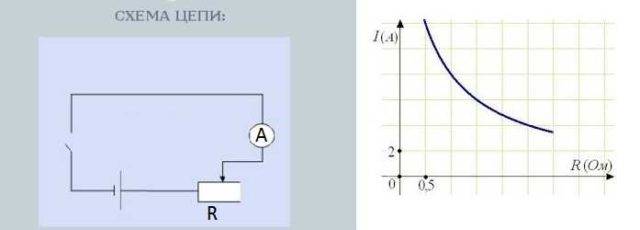
प्रतिरोध पर धारा की निर्भरता के परीक्षण के लिए परिपथ
रोकनेवाला घुंडी मोड़ने से प्रतिरोध बदल जाता है। उसी समय, एमीटर पर रीडिंग, जो वर्तमान ताकत को मापती है, भी बदल जाती है। इसके अलावा, प्रतिरोध जितना अधिक होगा, तीर उतना ही कम विचलित होगा - कम धारा। प्रतिरोध जितना कम होगा, तीर उतना ही विचलित होगा - करंट अधिक होगा।
प्रतिरोध पर करंट की निर्भरता लगभग रैखिक होती है, अर्थात यह ग्राफ पर लगभग सीधी रेखा के रूप में परिलक्षित होती है। लगभग क्यों - इस पर अलग से चर्चा की जानी चाहिए, लेकिन यह एक और कहानी है।
प्रत्यावर्ती धारा के लिए ओम का नियम
एसी सर्किट की गणना करते समय, प्रतिरोध की अवधारणा के बजाय, "प्रतिबाधा" की अवधारणा पेश की जाती है। प्रतिबाधा को Z अक्षर से निरूपित किया जाता है, इसमें भार R . का सक्रिय प्रतिरोध शामिल होता हैएक और प्रतिक्रिया एक्स (या आरआर) यह साइनसॉइडल करंट (और किसी भी अन्य रूपों की धाराओं) के आकार और आगमनात्मक तत्वों के मापदंडों के साथ-साथ स्विचिंग कानूनों के कारण है:
- आगमनात्मक परिपथ में धारा तुरन्त नहीं बदल सकती है।
- एक समाई वाले सर्किट में वोल्टेज तुरंत नहीं बदल सकता है।
इस प्रकार, करंट वोल्टेज से पिछड़ने या आगे बढ़ने लगता है, और स्पष्ट शक्ति सक्रिय और प्रतिक्रियाशील में विभाजित हो जाती है।
यू = मैं / जेड
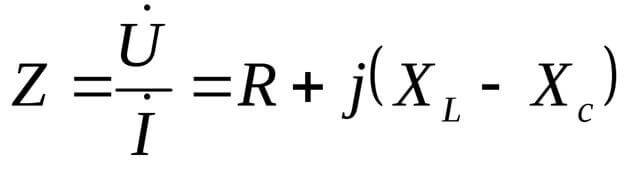
एक्सली और एक्ससी भार के प्रतिक्रियाशील घटक हैं।
इस संबंध में, मूल्य cosФ पेश किया गया है:
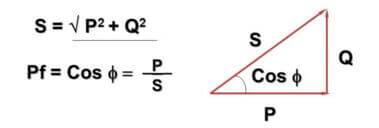
यहाँ - Q - प्रत्यावर्ती धारा और आगमनात्मक-कैपेसिटिव घटकों के कारण प्रतिक्रियाशील शक्ति, P - सक्रिय शक्ति (सक्रिय घटकों में नष्ट), S - स्पष्ट शक्ति, cosФ - शक्ति कारक।
आपने देखा होगा कि सूत्र और उसका निरूपण पाइथागोरस प्रमेय के साथ प्रतिच्छेद करता है। यह सच है और कोण Ф इस बात पर निर्भर करता है कि भार का प्रतिक्रियाशील घटक कितना बड़ा है - यह जितना बड़ा होगा, उतना ही बड़ा होगा।व्यवहार में, यह इस तथ्य की ओर जाता है कि वास्तव में नेटवर्क में प्रवाहित होने वाली धारा घरेलू मीटर से अधिक है, जबकि उद्यम पूरी शक्ति के लिए भुगतान करते हैं।
इस मामले में, प्रतिरोध को जटिल रूप में प्रस्तुत किया जाता है:
यहाँ j एक काल्पनिक इकाई है, जो समीकरणों के जटिल रूप के लिए विशिष्ट है। कम सामान्यतः i के रूप में संदर्भित किया जाता है, लेकिन इलेक्ट्रिकल इंजीनियरिंग में, प्रत्यावर्ती धारा के प्रभावी मूल्य को भी निरूपित किया जाता है, इसलिए भ्रमित न होने के लिए, j का उपयोग करना बेहतर होता है।
काल्पनिक इकाई √-1 है। यह तर्कसंगत है कि चुकता करते समय ऐसी कोई संख्या नहीं होती है, जिसके परिणामस्वरूप "-1" का नकारात्मक परिणाम हो सकता है।
जब ओम का नियम होता है
आदर्श परिस्थितियाँ बनाना आसान नहीं है। शुद्ध कंडक्टरों में भी, विद्युत प्रतिरोध तापमान के साथ बदलता रहता है। इसकी कमी क्रिस्टल जाली के अणुओं की गतिविधि को कम करती है, जो मुक्त आवेशों की गति को सरल बनाती है। "ठंड" के एक निश्चित स्तर पर अतिचालकता का प्रभाव होता है। गर्म करने पर विपरीत प्रभाव (चालकता का ह्रास) देखा जाता है।
इसी समय, इलेक्ट्रोलाइट्स, धातु और कुछ प्रकार के सिरेमिक वर्तमान घनत्व की परवाह किए बिना विद्युत प्रतिरोध बनाए रखते हैं। एक निश्चित तापमान शासन को बनाए रखते हुए मापदंडों की स्थिरता अतिरिक्त सुधारों के बिना ओम के नियम के सूत्रों को लागू करना संभव बनाती है।
सेमीकंडक्टर सामग्री और गैसों को अलग-अलग विद्युत प्रतिरोध की विशेषता है। यह पैरामीटर नियंत्रण मात्रा में वर्तमान तीव्रता से काफी प्रभावित होता है। प्रदर्शन विशेषताओं की गणना करने के लिए, विशेष गणना विधियों को लागू किया जाना चाहिए।
यदि प्रत्यावर्ती धारा पर विचार किया जाता है, तो गणना पद्धति को सही किया जाता है।इस मामले में, प्रतिक्रियाशील घटकों की उपस्थिति को ध्यान में रखना होगा। प्रतिरोध की प्रतिरोधक प्रकृति के साथ, ओम के नियम के सूत्रों के आधार पर गणना की जाने वाली तकनीकों को लागू करना संभव है।
किरचॉफ के नियम।
वितरण
विद्युत परिपथ की शाखाओं में धाराएं
किरचॉफ के प्रथम नियम का पालन करता है,
और वर्गों पर तनाव का वितरण
श्रृंखला किरचॉफ के दूसरे नियम का पालन करती है।
किरचॉफ के नियम
ओम के नियम के साथ-साथ प्रमुख हैं
विद्युत सर्किट के सिद्धांत में।
सबसे पहला
किरचॉफ का नियम:
बीजगणितीय
नोड में धाराओं का योग शून्य है:
मैं
= 0 (19)
कहाँ पे
मैं
किसी दिए गए नोड में परिवर्तित होने वाली शाखाओं की संख्या है।
यानी सारांश
शाखाओं में धाराओं तक फैली हुई है,
जो माना में अभिसरण करता है
नोड.
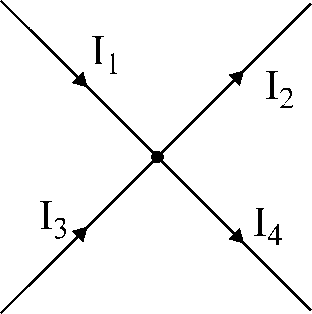
चित्र.17. चित्रण
किरचॉफ के पहले कानून के लिए।
संख्या
पहले के अनुसार संकलित समीकरण
किरचॉफ का नियम सूत्र द्वारा निर्धारित किया जाता है:
नुपू
= नु
– 1,
कहाँ पे
न्यू
माना श्रृंखला में नोड्स की संख्या है।
में धाराओं के संकेत
समीकरणों को चयनित को ध्यान में रखते हुए लिया जाता है
सकारात्मक दिशा। पर संकेत
धाराएं समान हैं यदि धाराएं समान हैं
इसके सापेक्ष उन्मुख
नोड.
उदाहरण के लिए,
चित्र 17 में दिखाए गए नोड के लिए:
हम नोड में बहने वाली धाराओं को संकेत देते हैं
"+", और नोड से बहने वाली धाराओं के लिए - संकेत
«-».
फिर समीकरण
किरचॉफ के पहले नियम के अनुसार लिखा जाएगा
इसलिए:
मैं1
- मैं2
+ मैं3
- मैं4
= 0.
समीकरण,
किरचॉफ के पहले नियम के अनुसार संकलित,
नोड्स कहलाते हैं।
इस
कानून इस तथ्य को व्यक्त करता है कि नोड में
इलेक्ट्रिक चार्ज जमा नहीं होता है
और इसका सेवन नहीं किया जाता है। बिजली की मात्रा
साइट पर आने वाले शुल्क योग के बराबर हैं
एक और एक ही में नोड छोड़ने के आरोप
समय की समान अवधि।
दूसरा
किरचॉफ का नियम:
बीजगणितीय
ईएमएफ का योग किसी भी बंद सर्किट में
श्रृंखला फॉल्स के बीजीय योग के बराबर है
इस सर्किट के तत्वों पर वोल्टेज:
यूआई
=
ईआई
IiRi=Ei(20)
कहाँ पे
मैं
- तत्व संख्या (प्रतिरोध या
वोल्टेज स्रोत) माना जाता है
रूपरेखा
**संख्या
दूसरे के अनुसार संकलित समीकरण
किरचॉफ का नियम सूत्र द्वारा निर्धारित किया जाता है:
नुपू
= नायब
- नु
+ 1 - नेड.एस.
कहाँ पे
नायब
- विद्युत परिपथ की शाखाओं की संख्या;
न्यू
- नोड्स की संख्या;
नेड.एस.
आदर्श ईएमएफ स्रोतों की संख्या है।
चित्र.18. चित्रण
किरचॉफ के दूसरे नियम के लिए।
के लिये,
दूसरे नियम को सही ढंग से लिखने के लिए
किसी दिए गए समोच्च के लिए किरचॉफ, इस प्रकार है
निम्नलिखित नियमों का पालन करें:
-
मनमाने ढंग से
समोच्च बाईपास की दिशा का चयन करें,
उदाहरण के लिए, दक्षिणावर्त (चित्र। 18)। -
ईएमएफ
और वोल्टेज गिरता है जो मेल खाता है
चयनित दिशा के साथ दिशा में
बाईपास को के साथ एक व्यंजक में लिखा जाता है
साइन "+"; यदि ई.एफ.एस. और वोल्टेज ड्रॉप
दिशा से मेल नहीं खाता
समोच्च, फिर वे एक संकेत से पहले होते हैं
«-».
उदाहरण के लिए,
चित्र 18 की रूपरेखा के लिए, किरचॉफ का दूसरा नियम
इस प्रकार लिखा जाएगा:
यू1
- उ2
+ यू3
=ई1
- इ3
- इ4
(21)
समीकरण (20) हो सकता है
के रूप में फिर से लिखें:
(यूआई
- ईई)
= 0 (22)
कहाँ पे
(यू
- इ)
- शाखा पर तनाव।
फलस्वरूप,
किरचॉफ का दूसरा नियम तैयार किया जा सकता है
इस अनुसार:
बीजगणितीय
किसी में शाखाओं पर वोल्टेज का योग
बंद लूप शून्य है।
संभावना
पहले चर्चा किया गया आरेख कार्य करता है
दूसरे की चित्रमय व्याख्या
किरचॉफ का नियम।
टास्क नंबर 1.
पर
अंजीर में सर्किट। 1 को धाराएं I दी गई हैं1
और मैं3,
प्रतिरोध और ईएमएफ धाराओं का निर्धारण करें
मैं4,
मैं5,
मैं6
; बिंदुओं के बीच वोल्टेज a
और बी
यदि मैं1
= 10mA,
मैं3
= -20 एमए,
आर4
= 5kOhm,
इ5
= 20बी,
आर5
= 3kOhm,
इ6
= 40बी,
आर6
= 2kOhm।
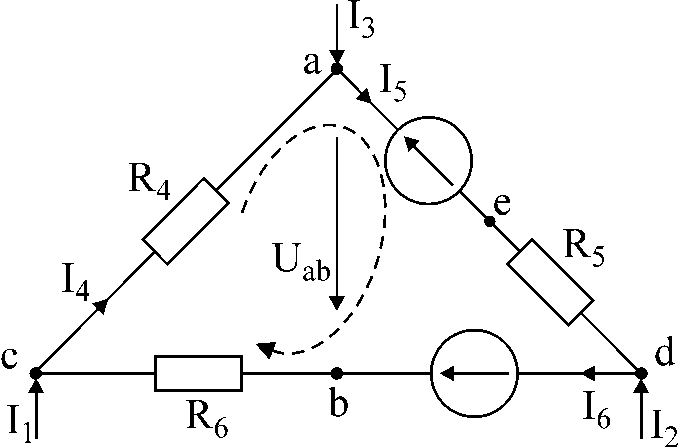
चित्र एक
समाधान:
-
किसी प्रदत्त के लिए
समोच्च, हम के अनुसार दो समीकरण बनाते हैं
किरचॉफ का पहला नियम और एक - के अनुसार
दूसरा। कंटूर दिशा
एक तीर द्वारा इंगित।

पर
समाधान के परिणामस्वरूप हमें मिलता है: I6
= 0; मैं4
= 10mA;
मैं5
= -10mA
-
पूछना
बिंदुओं के बीच वोल्टेज दिशा
एक
और बी
बिंदु "ए" से
"बी" इंगित करने के लिए
— उअब.
यह वोल्टेज समीकरण से पाया जा सकता है
किरचॉफ का दूसरा नियम:
मैं4आर4
+ यूअब
+ मैं6आर6
= 0
यूअब
= - 50 वी।
टास्क नंबर 2.
के लिये
अंजीर में चित्र। 2 के अनुसार समीकरण बनाएं
किरचॉफ के नियम और अज्ञात का निर्धारण
अंक।
दिया गया:
मैं1
= 20mA;
मैं2
= 10mA
आर1
= 5kOhm,
आर3
= 4kOhm,
आर4
= 6kOhm,
आर5
= 2kOhm,
आर6
= 4kΩ।
रेखा चित्र नम्बर 2
समाधान:
नोड्स की संख्या
समीकरण - 3, समोच्च समीकरणों की संख्या
– 1.
याद है!
दूसरे के अनुसार समीकरण संकलित करते समय
किरचॉफ का नियम, हम समोच्च चुनते हैं, में
जिसमें वर्तमान स्रोत शामिल नहीं हैं।
समोच्च की दिशा आकृति में इंगित की गई है।
पर
इस सर्किट की, शाखाओं की धाराएं I1
और मैं2.
अनजान
धाराओं
मैं3,
मैं4,
मैं5,
मैं6.

निर्णय लेने से
प्रणाली, हम प्राप्त करते हैं: I3
= 13.75 एमए;
मैं4
= -3.75mA;
मैं5
= 6.25mA;
मैं6
= 16.25mA।
मूल अवधारणा
विद्युत धारा प्रवाहित होती है जब एक बंद सर्किट इलेक्ट्रॉनों को सर्किट में उच्च क्षमता से कम क्षमता में स्थानांतरित करने की अनुमति देता है। दूसरे शब्दों में, करंट को इलेक्ट्रॉनों के एक स्रोत की आवश्यकता होती है जिसमें उन्हें गति में सेट करने की ऊर्जा होती है, साथ ही उनके नकारात्मक चार्ज की वापसी का एक बिंदु होता है, जो उनकी कमी की विशेषता होती है। एक भौतिक घटना के रूप में, एक सर्किट में करंट को तीन मूलभूत मात्राओं की विशेषता होती है:
- वोल्टेज;
- वर्तमान ताकत;
- एक कंडक्टर का प्रतिरोध जिसके माध्यम से इलेक्ट्रॉन चलते हैं।
ताकत और तनाव
वर्तमान ताकत (I, एम्पीयर में मापा जाता है) समय की प्रति यूनिट सर्किट में एक जगह से गुजरने वाले इलेक्ट्रॉनों (आवेश) की मात्रा है।दूसरे शब्दों में, माप I गति में इलेक्ट्रॉनों की संख्या का निर्धारण है
यह समझना महत्वपूर्ण है कि यह शब्द केवल गति को संदर्भित करता है: स्थिर शुल्क, उदाहरण के लिए, एक असंबद्ध बैटरी के टर्मिनलों पर, I का औसत दर्जे का मान नहीं होता है। एक दिशा में बहने वाली धारा को प्रत्यक्ष (DC) कहा जाता है, और समय-समय पर दिशा बदलने को प्रत्यावर्ती (AC) कहते हैं। वोल्टेज को इस तरह की घटना द्वारा दबाव के रूप में या गुरुत्वाकर्षण के प्रभाव में वस्तुओं की संभावित ऊर्जा में अंतर के रूप में चित्रित किया जा सकता है
इस असंतुलन को पैदा करने के लिए, आपको पहले ऊर्जा खर्च करनी होगी, जो उपयुक्त परिस्थितियों में गति में महसूस होगी। उदाहरण के लिए, ऊंचाई से लोड के गिरने पर, इसे उठाने के लिए काम किया जाता है, गैल्वेनिक बैटरी में, टर्मिनलों पर संभावित अंतर रासायनिक ऊर्जा के रूपांतरण के कारण उत्पन्न होता है, जनरेटर में - के संपर्क में आने के परिणामस्वरूप एक विद्युत चुम्बकीय क्षेत्र
तनाव को इस तरह की घटना द्वारा दबाव के रूप में या गुरुत्वाकर्षण के प्रभाव में वस्तुओं की संभावित ऊर्जा में अंतर के रूप में चित्रित किया जा सकता है। इस असंतुलन को पैदा करने के लिए, आपको पहले ऊर्जा खर्च करनी होगी, जो उपयुक्त परिस्थितियों में गति में महसूस होगी। उदाहरण के लिए, ऊंचाई से भार के गिरने पर, इसे उठाने का कार्य महसूस होता है, गैल्वेनिक बैटरी में टर्मिनलों पर संभावित अंतर रासायनिक ऊर्जा के रूपांतरण के कारण उत्पन्न होता है, जनरेटर में - एक के संपर्क में आने के परिणामस्वरूप विद्युत चुम्बकीय।
कंडक्टर प्रतिरोध
एक साधारण चालक कितना भी अच्छा क्यों न हो, यह इलेक्ट्रॉनों को उनके आंदोलन के कुछ प्रतिरोध के बिना कभी भी गुजरने नहीं देगा।प्रतिरोध को यांत्रिक घर्षण के एक एनालॉग के रूप में माना जा सकता है, हालांकि यह तुलना सही नहीं होगी। जब एक कंडक्टर के माध्यम से करंट प्रवाहित होता है, तो कुछ संभावित अंतर ऊष्मा में परिवर्तित हो जाता है, इसलिए रोकनेवाला के आर-पार हमेशा वोल्टेज गिरता रहेगा। इलेक्ट्रिक हीटर, हेयर ड्रायर और इसी तरह के अन्य उपकरणों को पूरी तरह से गर्मी के रूप में विद्युत ऊर्जा को नष्ट करने के लिए डिज़ाइन किया गया है।
सरलीकृत प्रतिरोध (R के रूप में निरूपित) एक माप है कि एक सर्किट में इलेक्ट्रॉनों का प्रवाह कितना धीमा है। इसे ओम में मापा जाता है। एक रोकनेवाला या अन्य तत्व की चालकता दो गुणों से निर्धारित होती है:
- ज्यामिति;
- सामग्री।
आकार का अत्यधिक महत्व है, जैसा कि हाइड्रोलिक सादृश्य से स्पष्ट है: एक लंबे और संकीर्ण पाइप के माध्यम से पानी को धकेलना एक छोटे और चौड़े पाइप के माध्यम से पानी को धकेलने की तुलना में बहुत कठिन है। सामग्री निर्णायक भूमिका निभाती है। उदाहरण के लिए, इलेक्ट्रॉन तांबे के तार में स्वतंत्र रूप से घूम सकते हैं, लेकिन रबर जैसे इन्सुलेटर के माध्यम से बिल्कुल भी प्रवाह नहीं कर सकते, चाहे उनका आकार कुछ भी हो। ज्यामिति और सामग्री के अलावा, अन्य कारक भी हैं जो चालकता को प्रभावित करते हैं।
ओम के नियम की व्याख्या
आवेशों की गति सुनिश्चित करने के लिए, आपको परिपथ को बंद करना होगा। अतिरिक्त शक्ति के अभाव में, करंट लंबे समय तक मौजूद नहीं रह सकता है। संभावनाएं जल्दी बराबर हो जाएंगी। सर्किट के ऑपरेटिंग मोड को बनाए रखने के लिए, एक अतिरिक्त स्रोत (जनरेटर, बैटरी) की आवश्यकता होती है।
पूरे सर्किट में सभी घटकों का कुल विद्युत प्रतिरोध होगा। सटीक गणना के लिए, कंडक्टरों में नुकसान, प्रतिरोधक तत्वों और एक शक्ति स्रोत को ध्यान में रखा जाता है।
एक निश्चित वर्तमान शक्ति के लिए कितने वोल्टेज को लागू करने की आवश्यकता है, इसकी गणना सूत्र द्वारा की जाती है:
यू = मैं * आर।
इसी तरह, माना संबंधों की मदद से, सर्किट के अन्य पैरामीटर निर्धारित किए जाते हैं।
समानांतर और सीरियल कनेक्शन
इलेक्ट्रिक्स में, तत्व या तो श्रृंखला में जुड़े होते हैं - एक के बाद एक, या समानांतर में - यह तब होता है जब कई इनपुट एक बिंदु से जुड़े होते हैं, और एक ही तत्व से आउटपुट दूसरे से जुड़े होते हैं।
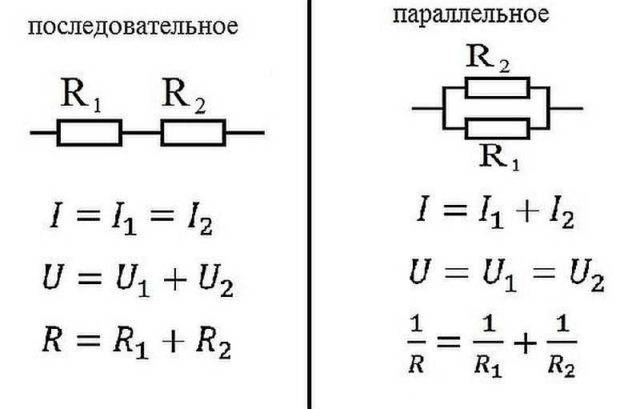
समानांतर और श्रृंखला कनेक्शन के लिए ओम का नियम
सीरियल कनेक्शन
इन मामलों के लिए ओम का नियम कैसे काम करता है? श्रृंखला में जुड़े होने पर, तत्वों की श्रृंखला के माध्यम से बहने वाली धारा समान होगी। श्रृंखला में जुड़े तत्वों के साथ एक सर्किट के एक खंड के वोल्टेज की गणना प्रत्येक खंड में वोल्टेज के योग के रूप में की जाती है। इसे कैसे समझाया जा सकता है? किसी तत्व के माध्यम से धारा का प्रवाह उसके एक भाग से दूसरे भाग में आवेश के भाग का स्थानांतरण है। मेरा मतलब है, यह कुछ काम है। इस काम का परिमाण तनाव है। यह तनाव का भौतिक अर्थ है। यदि यह स्पष्ट है, तो हम आगे बढ़ते हैं।
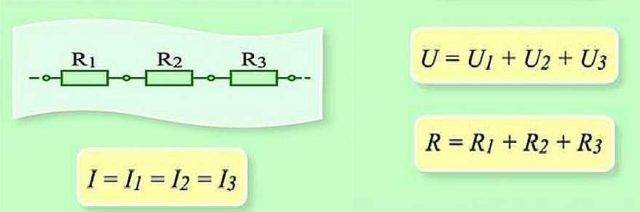
सर्किट के इस खंड के सीरियल कनेक्शन और पैरामीटर
श्रृंखला में जुड़े होने पर, प्रत्येक तत्व के माध्यम से चार्ज को बारी-बारी से स्थानांतरित करना आवश्यक है। और प्रत्येक तत्व पर यह काम का एक निश्चित "मात्रा" है। और श्रृंखला के पूरे खंड पर काम की मात्रा का पता लगाने के लिए, आपको प्रत्येक तत्व पर काम जोड़ने की जरूरत है। तो यह पता चला है कि कुल वोल्टेज प्रत्येक तत्व पर वोल्टेज का योग है।
इसी प्रकार - जोड़ की सहायता से - परिपथ खंड का कुल प्रतिरोध भी पाया जाता है। आप इसकी कल्पना कैसे कर सकते हैं? तत्वों की श्रृंखला के माध्यम से बहने वाली धारा क्रमिक रूप से सभी प्रतिरोधों पर विजय प्राप्त करती है। एक क। अर्थात्, उस प्रतिरोध का पता लगाने के लिए जिस पर उसने विजय प्राप्त की, प्रतिरोधों को जोड़ना आवश्यक है। कमोबेश ऐसे ही।गणितीय व्युत्पत्ति अधिक जटिल है, और इस कानून के तंत्र को समझना आसान है।
समानांतर कनेक्शन
एक समानांतर कनेक्शन तब होता है जब कंडक्टरों / तत्वों की शुरुआत एक बिंदु पर होती है, और दूसरे पर उनके सिरे जुड़े होते हैं। हम उन नियमों की व्याख्या करने का प्रयास करेंगे जो इस प्रकार के यौगिकों के लिए मान्य हैं। चलो करंट से शुरू करते हैं। तत्वों के कनेक्शन बिंदु पर कुछ परिमाण की धारा की आपूर्ति की जाती है। यह अलग हो जाता है, सभी कंडक्टरों के माध्यम से बहता है। इससे हम यह निष्कर्ष निकालते हैं कि खंड में कुल धारा प्रत्येक तत्व में धारा के योग के बराबर है: I = I1 + I2 + I3।
अब वोल्टेज के लिए। यदि वोल्टेज चार्ज को स्थानांतरित करने के लिए काम करता है, तो एक चार्ज को स्थानांतरित करने के लिए आवश्यक कार्य किसी भी तत्व पर समान होगा। यानी प्रत्येक समानांतर जुड़े हुए तत्व पर वोल्टेज समान होगा। यू=यू1=यू2=यू3. एक श्रृंखला खंड के लिए ओम के नियम की व्याख्या के मामले में उतना मजेदार और दृश्य नहीं है, लेकिन आप समझ सकते हैं।
समानांतर कनेक्शन के लिए कानून
प्रतिरोध के लिए, चीजें थोड़ी अधिक जटिल हैं। आइए चालकता की अवधारणा का परिचय दें। यह एक विशेषता है जो इंगित करती है कि इस कंडक्टर के माध्यम से चार्ज करना कितना आसान या मुश्किल है। यह स्पष्ट है कि प्रतिरोध जितना कम होगा, करंट को पास करना उतना ही आसान होगा। इसलिए, चालकता - जी - की गणना प्रतिरोध के पारस्परिक के रूप में की जाती है। सूत्र में, यह इस तरह दिखता है: G = 1/R।
हम चालकता के बारे में क्यों बात कर रहे हैं? क्योंकि तत्वों के समानांतर कनेक्शन वाले अनुभाग की कुल चालकता प्रत्येक अनुभाग के लिए चालकता के योग के बराबर होती है। G = G1 + G2 + G3 - समझने में आसान। समानांतर तत्वों के इस नोड को कितनी आसानी से पार कर जाएगा यह प्रत्येक तत्व की चालकता पर निर्भर करता है। तो यह पता चला है कि उन्हें मोड़ने की जरूरत है।
अब हम प्रतिरोध के लिए आगे बढ़ सकते हैं।चूंकि चालकता प्रतिरोध का व्युत्क्रम है, इसलिए हम निम्नलिखित सूत्र प्राप्त कर सकते हैं: 1/R = 1/R1 + 1/R2 + 1/R3।
क्या हमें समानांतर और सीरियल कनेक्शन देता है?
सैद्धांतिक ज्ञान अच्छा है, लेकिन इसे व्यवहार में कैसे लागू किया जाए? किसी भी प्रकार के तत्वों को समानांतर और श्रृंखला में जोड़ा जा सकता है। लेकिन हमने रैखिक तत्वों का वर्णन करने वाले केवल सबसे सरल सूत्रों पर विचार किया। रैखिक तत्व प्रतिरोध होते हैं, जिन्हें "प्रतिरोधक" भी कहा जाता है। तो यहां बताया गया है कि आपने जो सीखा है उसका उपयोग कैसे कर सकते हैं:
यदि कोई बड़ा-मान प्रतिरोधी उपलब्ध नहीं है, लेकिन कई छोटे हैं, तो श्रृंखला में कई प्रतिरोधों को जोड़कर वांछित प्रतिरोध प्राप्त किया जा सकता है। जैसा कि आप देख सकते हैं, यह एक उपयोगी तकनीक है।
बैटरी के जीवन का विस्तार करने के लिए, उन्हें समानांतर में जोड़ा जा सकता है। इस मामले में वोल्टेज, ओम के नियम के अनुसार, वही रहेगा (आप मल्टीमीटर के साथ वोल्टेज को मापकर सुनिश्चित कर सकते हैं)। और दोहरी बैटरी का "जीवनकाल" दो तत्वों की तुलना में बहुत लंबा होगा जो एक दूसरे को प्रतिस्थापित करेंगे
बस ध्यान दें: समान क्षमता वाली केवल बिजली आपूर्ति को समानांतर में जोड़ा जा सकता है। यानी एक डेड और नई बैटरी को कनेक्ट नहीं किया जा सकता है।
यदि आप अभी भी कनेक्ट करते हैं, तो जिस बैटरी का चार्ज अधिक है, वह कम चार्ज वाली बैटरी को चार्ज करेगी। नतीजतन, उनका कुल शुल्क कम मूल्य पर गिर जाएगा।
सामान्य तौर पर, इन यौगिकों के लिए ये सबसे आम उपयोग हैं।
आदर्श ईएमएफ स्रोत
इलेक्ट्रोमोटिव बल (ई) एक भौतिक मात्रा है जो चार्ज वाहक के बंद सर्किट में आंदोलन पर बाहरी बलों के प्रभाव की डिग्री निर्धारित करती है। दूसरे शब्दों में, कंडक्टर के माध्यम से धारा कितनी दृढ़ता से प्रवाहित होती है यह ईएमएफ पर निर्भर करेगा।
ऐसी अतुलनीय घटनाओं की व्याख्या करते समय, घरेलू स्कूल के शिक्षक हाइड्रोलिक उपमाओं की विधि की ओर मुड़ना पसंद करते हैं। यदि एक कंडक्टर एक पाइप है, और विद्युत प्रवाह इसके माध्यम से बहने वाले पानी की मात्रा है, तो ईएमएफ वह दबाव है जो एक पंप तरल पदार्थ को पंप करने के लिए विकसित करता है।
इलेक्ट्रोमोटिव बल शब्द वोल्टेज जैसी अवधारणा से संबंधित है। वह, ईएमएफ, वोल्ट (इकाई - "वी") में भी मापा जाता है। प्रत्येक शक्ति स्रोत, चाहे वह बैटरी हो, जनरेटर हो या सौर पैनल, का अपना इलेक्ट्रोमोटिव बल होता है। अक्सर यह EMF आउटपुट वोल्टेज (U) के करीब होता है, लेकिन हमेशा इससे थोड़ा कम होता है। यह स्रोत के आंतरिक प्रतिरोध के कारण होता है, जिस पर वोल्टेज का हिस्सा अनिवार्य रूप से गिरता है।
इस कारण से, ईएमएफ का आदर्श स्रोत एक अमूर्त अवधारणा या भौतिक मॉडल है जिसका वास्तविक दुनिया में कोई स्थान नहीं है, क्योंकि बैटरी रिन का आंतरिक प्रतिरोध, हालांकि बहुत कम है, फिर भी पूर्ण शून्य से अलग है।
ईएमएफ का आदर्श और वास्तविक स्रोत
विभेदक रूप में
सूत्र को अक्सर एक विभेदक रूप में प्रस्तुत किया जाता है, क्योंकि कंडक्टर आमतौर पर अमानवीय होता है और इसे सबसे छोटे संभव वर्गों में तोड़ना आवश्यक होगा। इससे गुजरने वाली धारा परिमाण और दिशा से जुड़ी होती है, इसलिए इसे अदिश राशि माना जाता है। जब भी किसी तार के माध्यम से परिणामी धारा ज्ञात की जाती है, तो सभी अलग-अलग धाराओं का बीजगणितीय योग लिया जाता है। चूँकि यह नियम केवल अदिश राशियों पर लागू होता है, धारा को भी अदिश राशि के रूप में लिया जाता है। यह ज्ञात है कि धारा dI = jdS खंड से होकर गुजरती है। उस पर वोल्टेज एडल है, फिर एक स्थिर क्रॉस सेक्शन और समान लंबाई वाले तार के लिए, अनुपात सही होगा:
 विभेदक रूप
विभेदक रूप
इसलिए, सदिश रूप में धारा का व्यंजक होगा: j = E.
महत्वपूर्ण! धातु चालकों के मामले में, बढ़ते तापमान के साथ चालकता कम हो जाती है, जबकि अर्धचालकों के लिए यह बढ़ जाती है। ओमोव का नियम सख्त आनुपातिकता प्रदर्शित नहीं करता है
धातुओं और मिश्र धातुओं के एक बड़े समूह का प्रतिरोध परम शून्य के करीब तापमान पर गायब हो जाता है, और इस प्रक्रिया को अतिचालकता कहा जाता है।